3 Common Subtraction Strategies

Jen Moffett, , 2 Comments

A dear friend had this posted last night:

1509183_10208482214599412_3676246263346474226_nWhy?! Why would I even consider doing simple subtraction like this?! It’s about 10 steps too many, not to mention super confusing!!!

And to be honest, I had to look at the first problem (represented as a “tape diagram”) to figure out what they were asking.  So my next blog will be about the difference between CCSS standards and how they are being implemented (often poorly). Today is to help out my friend…

So, back in the day we were given a set of procedures to follow step-by-step. We never really knew why (or at least I didn’t): just follow the magical steps in order and it will produce a number that your teacher will smile at and say you are smart. If you did not follow the steps correctly, then have fun with extra practice and staying in during lunch.

CCSS is reversing this. They are allowing students (through research-based strategies kids naturally use) to explore a variety of ways to solve problems. From there, in grade 4 they will generate the traditional algorithm. It hasn’t gone away; it is just the end of the journey.

Here are 3 of the most used strategies for kiddos in subtraction.

1. Count Up. Makes sense. We spend so much time teaching how to add. Why not use it? A subtraction problem is considered a “missing addend” problem.

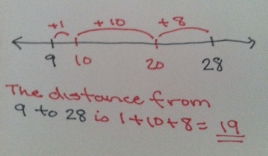
One of the ways to represent counting up is on an open number line. This is the one the above pic shows on a tape diagram. So you are finding how far (the distance between) it is from one value to the next.

Typically, kids will add up to the nearest ten, then hundred, and jump until they get to the number they need. Add up all of the “hops” you did and that is the distance.

28 - 9 number line

28 – 9

Think about it as, “What plus 9 makes 28?”

Or  “How far must I go to get from 9 to 28?”

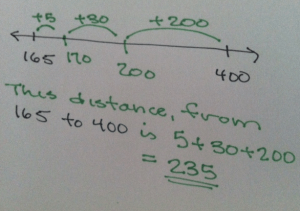
400 - 165 number line

400-165

Think about it as “What plus 165 makes 400?”

Or “How far do I have to go to get from 165 to 400?”

This is my favorite strategy, because it takes the “borrowing” out of the math. (Why is it called “borrowing”? You will never give it back.)

2. Decompose the subtrahend. Name it what you want. You will break apart the second number in the subtraction problem to make it easier to subtract. This is typically shown by a number bond.

28 - 9 number bond28 – 9     

Break apart the 9 into 8 and 1. (9 = 8+1)

This allows the student to subtract the same amount of ones from ones first (8 – 8). The leftover ones (in this case, 1) can be taken away second. Again, a great strategy when the subtrahend (the second number in the subtraction problem) has a digit larger than the minuhend (the first number).

400 - 165 number bond

400-165

Break apart the 165 by place value (165 = 100+60+5).

This is typically a strategy that works well in your head, versus the complexity of seeing it written out mathematically. Trust me when I say that kids can do this quickly in their head; writing what they did is much harder (and much harder for us to figure out what the heck they did). You do have to know the ways to make 10’s and 100’s. So I have to know that 60 + 40 = 100 (or 6 tens + 4 tens = 10 tens = 100) to know that 300 – 60 = 240. This is the second grade standard; subtracting multiples of tens. (BTW: This is the one that gets blasted on Facebook. I have seen students use this strategy in their head time and time again. The minute we record their thinking mathematically, people get all out of whack. It is not more steps than the standard algorithm. The moves you make are written as equations using place value rather than little meaningless tick marks at the top of the problem.

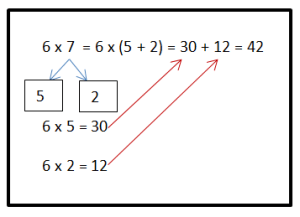
 3. Solve using place value. Similar to the second strategy, but you can break both numbers up as you choose.

28 - 9 decompose28 – 9

Again, looks a lot scarier when I record it this way. Using a number bond is a great visual, and typically the student starts this process by just saying what they want to subtract verbally, rather than writing all of the notation down.

400 - 165 decompose400 – 165

I am just showing one way to break apart the values. When I asked my son how he would do it, he said he would break up 400 into 100 + 100 + 200. That made sense to him, and in the end that is what we want. For students to use a strategy and make sense of it.

You will find that one strategy works with the numbers given better than another. For example, with the 400 – 165, I would use a counting up. With 28 – 9, I like the break up the subtrahend. The point of it all is for students to really understand what is happening when they subtract. Where is the “borrowing” or “regrouping” happening, so when they learn the traditional algorithm, it is an extension of their learning rather than some random tick mark step-by-step formula.

Continue reading “3 Common Subtraction Strategies” →

3 Common Subtraction Strategies

Why Distribute in Third Grade?

Jen Moffett, , Leave a comment

I am blessed to work with dedicated teachers who care deeply for their students and are working hard to understand the conceptual shifts CCSS brings to the table in math. One such teacher emailed me this weekend distraught, not knowing how to respond to a frustrated parent. The premise was the mother did not understand why her third grader was being asked to learn the distributive property, when she herself hadn’t learned it until Algebra I.

The arithmetic properties (commutative, associative, identities, etc.) were not created for Algebra I, though many of us didn’t learn them until then. I remember thinking that a bunch of old guys must have made them up for the sheer joy of torturing me into memorizing random stuff. No, the properties are the rules that give us the freedom to simplify math problems to make them easier to calculate while keeping the value the same.

An example. Which would be easier to solve in your head, 15 + 29 then add 5  OR  15 + 5 then add 29? The second, because we can make tens (15+5 = 20) and easily add 29 to it rather than have to “carry the 1” on the first example. This illustrates the commutative property: when adding or multiplying, I can perform that operation with any numbers in the problem first. I can switch the numbers around to make the problem easier to add (or multiply).

These properties should be celebrated as early as Kindergarten. Students do not necessarily need to know the names, but should realize through exploration that they exist and help them find their values.

Back to the distributive property. We old-timers saw it used like this: 6(5x + 2) = 30x + 12. This is not what we are asking third graders to do! Since the CCSSM standards require single digit multiplication fluency in third grade (1×1 through 9×9), it is natural to teach the distributive property at this level. This property allows me to break up one of my bigger numbers into parts. I can then multiply those smaller parts by the other factor to make it easier.

6 x 7 arrayExample: 6 x 7   This is always a toughie. Is it 48? 42? 56? I don’t know! Even if I draw an array (the above pic), that is a whole lot of dots to count!

But if I know my 5’s and 2’s, I can figure it out using the distributive property!             Break up the 7 into 5 and 2.   So now 6 x 7 becomes 6 x (5 + 2).    distribute array 6 x 7

I know 6 x 5 = 30.  (This is illustrated in yellow.)

I know 6 x 2 = 12 (This is illustrated in red.)

So 6 x (5 + 2) = 30 + 12 = 42.

distributive property 6 x 7

You may also see the distributive property used as a “number bond”. This is when it is broken up into parts, either using boxes or circles to show the parts. In this case, 7 is broken up into two parts:  5 and 2.

Utilizing the distributive property is an amazing strategy for students who struggle with memorization! They can use the distributive property to break up larger values they don’t know the multiplication facts for, until they have time to build fluency. More important, it teaches kids the value of knowing that math isn’t just memorization. There are structures and patterns that I can use. If I know the rules that govern those patterns (the properties), I can change the structure to find the value in an easier way. 

Why Distribute in Third Grade?

My Nightmare Learning Algorithms (And Why I Am Thrilled We Now Encourage Multiple Strategies!)

Jen Moffett, , 4 Comments

CCSS math debunkIf you are on Facebook, you have seen this (or one similar to it), usually followed by stating that a certain set of standards are evil and we should be teaching the kids drill and kill through the “right way”. So let’s clear the air (Or let me fill it with hot air and you can comment below. Bring it on!).

To start,  “our way” is not the way of all. The step and structure with which we add, subtract, multiply and divide are not used by all countries. In fact, these methods are just some of the many ways students can simplify problems using these four operations. The ones we traditionally use are examples of “algorithms”. If used correctly, each will work for different number types and you can get “the right answer” pretty quickly if you have had lots of practice with them.

CCSS math debunk 3BUT THEY ARE NOT THE ONLY ONES! And I would fight the good fight that there are MUCH easier ways to get to the value using other strategies. I will even throw myself under the bus and tell you that I do not use the traditional multiplication algorithm. I make too many mistakes when I use it. I know it, but there is another method that works just as fast for me, and I get the correct value using it. And long division? Ugh. Why not just start with something I know, chunk it out, and get to easier numbers??? May look a bit odd, but still it is faster than sitting there trying to find out how many times one value goes into another (More on this division idea in an upcoming post for all you 4-6th grade parents!).

So think back to your elementary days. How many days were spent drilling the algorithms you now know (or pretend to know since you use a calculator instead)? How many hours? For me, it was a nightmare. I didn’t get them. I didn’t know when to move a little 1 (And why was it so tiny if it meant a bigger number???) in addition, why we crossed out stuff on top and not only moved it over, but made a double digit number in subtraction (What happened to my little 1 friend in addition? Where did she go???), when to put an “X” and why the heck were we even using an X in multiplication when it isn’t even a number, and so on. I was confused, and I covered it up by checking with a calculator and fixing each line to pretend I knew what I was doing. It was horrible, and I felt stupid, slow and sad.

CCSS math debunk 2I had my a-ha moment in seventh grade. (So it took EIGHT YEARS to finally figure it out.) My math teacher took me out of science, my favorite class mind you, to have a double dose of math. (Great. Now I get to hate it twice as long.) However, he started showing me other ways to do the math. What other countries and cultures were using to figure out the exact same problems, but with visuals and graphic organizers and all kinds of craziness. It was wonderful. It was a breath of fresh air. It was my lifeline to true mathematics.

You see, math isn’t just about calculating. I think of mathematics as finding patterns and relationships in and among quantitative items, and using those patterns and relationships to create rules, strategies and “algorithms”, prove or disprove others (And my own!) rules and algorithms, and figure out how the world works on a quantitative scale. It is beautiful. It is elegant. It makes life make sense.

Keep in mind, the standards DO say for students to eventually use our traditional algorithms as ONE STRATEGY for finding the values. But it is at the end of their journey of understanding. It is the final step of a long walk through discovery; using manipulatives, moving to visual representations, conjecturing student-strategies (whether they work all the time or not), and finally moving into the algorithm you all claim to know and love.

puzzle piecesThink of a puzzle. My husband starts with the border. I start with the middle and the pieces that have the same color or object. Yet we will both finish the puzzle, even though we went at putting it together differently.  Some of the representations will be easy for your child, others a bit more difficult until they understand how they are relating to the operation. Yet, they will get to the end and finish the puzzle, even if his struggles are different than another’s. That is why working together is so important. We can help each other make sense and persevere to the end!

So, at the beginning of another school year, take a deep breath. Give different models and strategies a chance. Ask for help in understanding how the strategies or models work and their significance to understanding an operation (Send ME questions and problems!!!!). Encourage your child to try something new, and be supportive. As the child who needed something different, I thank you. 🙂

My Nightmare Learning Algorithms (And Why I Am Thrilled We Now Encourage Multiple Strategies!)

Helping Your Child With Math HW: Some Don’ts and A Lot of Do’s

Jen Moffett, , Leave a comment

The struggle is real. Your child is frustrated, you are frustrated, and the homework you both have been working on STILL is not complete. Your child screams, “You aren’t doing it RIGHT…That’s NOT how my teacher showed me…I HATE math!”

Here are the 2 mistakes we as parents make. Since it is the beginning of the school year, let’s really make an effort to abide by these Golden Rules. These are followed by helpful hints to make it a successful year in mathematics.

Golden Rule #1 (Even if you dislike math A LOT) Never Ever say negative remarks regarding your abilities in math or about math in general. I cannot tell you how many Student Study Team meetings began with a parent saying, “Well I was never good at math”…That is your golden ticket for your child to say the same thing, and think it is okay to just give up. It is not okay. Would you admit that you couldn’t read? No. So just don’t say it. Don’t say the homework is “stupid” or disrespect your child’s teacher in front of her. The results will not improve her performance or her efforts in her math class. If you have a problem with the mathematics coming home or with your child’s teacher, discuss it with the teacher.

 Golden Rule #2 Do not do your child’s homework for her. I often tutor my family and friends. My favorite comment is, “I don’t get (insert child’s name) math homework. Can you come explain it to me?” Though I would love you (the parent) to understand the mathematics as well, you should not be the one doing the work. Your child needs to do the work, needs to struggle and figure out where he is lost, and needs to feel what it’s like to finally “get it”. That is the goal of the homework, not just completing the problems.

Ways to Help Your Child With Mathematics

  1. Set a schedule. Your child should do his homework at a regular time each day. My son’s schedule is crazy: Cross Country in the am two days, in the pm two days, and Youth Group one night. Yet the schedule is the same every day. Whatever time he gets home, he eats something (whether it’s a snack or dinner) then gets down to homework. He knows this is the routine, so there is no griping.
  2. Set a standard place to complete HW. It is a pain, but I like him to do his homework at the dinner table. He can spread out, and I am usually fixing (or cleaning up) dinner nearby to ask questions when needed. We have a side tray table with materials he may need (paper, calculator, pencil, colored pencils, etc) set up for him so there is no reason to leave the space.
  3. Encourage. Encourage. Encourage. The students whom I hear the most from aren’t the ones who got it the fastest. They are the ones who put in the effort, with me cheering them on through their frustrations and never giving up on them or their learning mathematics. It means the world to your child to know you are rooting for them to be successful (Even if they won’t admit it!).
  4. Give directives/Ask questions FIRST. Here is a list of prompts and probing questions to move you along.
    • Tell me what you are doing (or working on).
    • What did you do in class that was like this problem? Do you have an example in your notes we can look at? Let’s re-read your notes and see if that helps you remember.
    • Could we call someone from your class? (This is great with social media. They can facetime, Skype, Google Hangout, etc. Get your kids to make study groups from friends in their classes!)
    • Let’s look in your math book and see if the examples from the section you are working on will help us.
    • Does your math book have video tutorials? (Most do! Get the login and password from your teacher BEFORE a crisis!) Let’s watch it and see if it helps us understand more.
    • What did you try first?
    • How did you get that answer? Explain it to me.
    • What is the pattern?
    • What doesn’t make sense? Where did you get stuck?
    • Does your teacher offer tutoring tomorrow morning? Let’s get you there!
  5. Email me the math! Love to blog about math problems in REAL time! jarguelovesmath@yahoo.com
  6. If none of this is helping, and your child has worked on her math homework for over 30 minutes will little (or no) understanding, STOP. I would email her math teacher and ask for advice. Explain the attempts made and where your child is stuck. Most teachers will be understanding and give her more time. If the teacher does not, request a meeting with just the two of you to discuss the difficulties your child is having and intervention options the teacher (or school) offers.

Good luck and have a great year support your child’s success in mathematics!

Helping Your Child With Math HW: Some Don’ts and A Lot of Do’s

Start Smart! 6 Things Your Child Can Do To Start The Year Right

Jen Moffett, , Leave a comment

You know it’s almost here! The smell of newly sharpened pencils and the odor of dry erase pens…The aisles of school supplies in the local stores…Sales on children’s clothing…School is upon us! Here are some tips for you to encourage your child to do to get the year off to a great start in their math class!

Greet the Teacher1. Greet your teacher the first day. I cannot stress the importance of making a good first impression. This is especially important in middle school, where we teachers have over 180 students to remember!  Encourage your child to make eye contact with his teacher and shake her hand. Say, “My name is ________ and I look forward to being in your class!”

2. Sit in the front! Now, some teachers choose your seats for you. If they do not, choose a seat in the first two rows. It forces you to listen, and you have first crack at your teacher if you don’t understand something.Sit in Front

3. S.L.A.N.T. This is a behavioral routine (I learned about it when I was an AVID teacher) used by many school districts to encourage positive engagement in class. (For more information, visit http://www.powayusd.com/teachers/lharvey/path/slant.htm)

S– Sit Up – Sitting with your feet flat on the floor, back straight, and facing forward focuses you and puts you in the right mindset to work and take part in discussions.            

L– Lean Forward- Leaning forward shows you are engaged in the lesson, which often encourages teachers to ask you questions, see how you are doing,  and keep you engaged.

A–Ask Questions- I can guarantee you are not the only one with your question. However, by being the bold one to ask it, the teacher knows you are listening and that you care. In turn, she will take more time with you to make sure you understand.

N–Nod Yes/No- The simple act of nodding when you agree/disagree lets the teacher know you are listening and what you are thinking.

T–Talk With Teachers- We are real people. Talk to us. The more we know you, the more we care about you.

HW4. Write your homework down. The most common reason I get for students not doing their HW is that they didn’t know what it was. Get in the habit of coming in and immediately pulling out your planner to write down your HW. When you do your HW, highlight it to indicate it is complete.

5. Do your homework! Start off right. Get in the habit of doing your HW. If you don’t understand it, try it for at least 20 minutes and email your teacher to let her know what you tried and where you got stuck. Just putting in the effort will let your teacher know you care. The more you care, the more we care about helping you.

6. Don’t be absent. Miss school, miss out. You simply cannot make up the discussions and learning that took place on a day you missed. The more school you miss, the more you don’t understand, the more you dislike school, the more likely you will drop out.Absent

Have a great first week of school!

Up next: Questions to Ask Your Child To Help With HW!

Start Smart! 6 Things Your Child Can Do To Start The Year Right

Beyond Counting: Ideas and Activites For Your Little Ones

Jen Moffett, , , , , , Leave a comment

While waiting for his big brother at the orthodontist, my little boy, C,  had the following conversation…

Dr. T: How old are you, cutie?

C: I’m three!

Dr. T: How old is your brother (pointing towards my thirteen year old)

C: Four!

This was such a proud mama moment for me!

Now you may ask yourself, “Why is she getting all excited over this? Clearly, he is not four. Why is she so proud of her little boy?”

There are a number of reasons why this is a critical step towards numeracy. I truly believe that if you start children purposefully thinking about numbers early on, their chance for success in mathematics increases dramatically. So let’s highlight a few of the big ideas C is working towards.

bears

1. Cardinality– This is the idea that the number being used is measuring some amount. It answers the question, “How many?” For example, I can ask my son, “How many bears do you see?” He would count them one by one until he got to the number six. That last number, 6, tells you the number of bears in the set. This is a big deal! The child is no longer counting from memorization; he is recognizing that the number relates to a certain amount of “things”. The more things you have, the further you have to count. C recognized that his brother was older (or “bigger”). Therefore, his brother was tagged to a number after the one he identified with, three. He did not know how many more to go, just that he had to choose a number beyond his own. Cool.

2. Inclusion– This is the idea that the number labeling “how many objects” in a group includes all of the preceding numbers. So even though we have six bears, we can also think of it as “one and some more”, “two and some more”, “three and some more”, and so on. This is critical for addition and subtraction. If I have the number 14, I can think about it as “ten and four more”, which helps me when I want to add or subtract and regroup to make the problem easier. C knew that his brother was older, and therefore had to include his age (three) and some more. Again, he isn’t at the point of knowing how much more, but is on his way. Awesome.

3. Magnitude– The size of the object. In this case, a number (or value) given to a quantity (age) for the purpose of comparing with another quantity. This idea is instrumental for estimation, particularly with very large and very small numbers. In fact, one of the posts requested of me to write is helping students compare fractions. If a child does not know the relative size of the number they are considering then it is very difficult to compare, operate or manipulate it with any real fluency or number sense. How do I know my answer is reasonable if I haven’t a clue what the numbers I am working with represent??? For C, he was able to recognize that his brother had to be a larger quantity than three, because he is older. Super rad!

These three ideas are certainly related, but each has a different feel. You can work with them simultaneously, so long as there is purpose to the questions and tasks you present to your kids. Below are some simple, but powerful, activities you can play with your little ones to build these concepts. I choose the games that you can take on the road, to the doctor’s office, to a restaurant, etc. Instead of sitting around being squirrelly, play a game while you wait. Even five minutes will have a significant impact!

1. Count and Check: Grab a handful of ANYTHING (balls, pennies, beans, cheerios, etc) and ask your child to count how many. Make sure the amount of objects is appropriate. (For example, C is working on objects through 5.) When he finishes counting the last object, ask, “How many _____ are there?” If he cannot answer, that is okay! He is working towards cardinality. He is able to say the objects one by one (which is called one to one correspondence), but hasn’t figured out that the last number he says represents the entire amount. Have him count again, and ask again. If he cannot answer again, say, “There are (say the amount) ______ here.”  You can play this at the grocery store (count the apples, bananas, etc), setting the table (How many forks?), etc.

2. Match Me! Grab a die (one dice) and a handful of ANYTHING in a baggie. (I typically do this with pennies at restaurant.) Have your child roll the die. Let’s say she rolls a five. She takes out that many pennies and lays them out for you to see. Ask her to count them one-by-one to make sure she has five. At the end ask, “How many pennies do you have?” If she doesn’t know, that is okay! Have her recount, then ask again. If she still isn’t able to tell you, say, “I see you have five pennies.” Make sure you roll next and model for your child. Take turns until you get bored or dinner comes!

To bring the difficulty up, after playing each of these, ask, “If I gave you one more item, how many would you have?” This brings in the concepts of magnitude and inclusion! If your child has to recount with one more added in, that is fine! You know he’s got it when he can answer quickly without physically adding in another item and recounting.

Need another level of difficulty? Ask, “If I took away one of the items, how many will be left?” Same idea, but working backwards, and just as important!

Beyond Counting: Ideas and Activites For Your Little Ones

Summer Math: Does It Make “Cents”?

Jen Moffett2 Comments

Summer is on the horizon! No more pencils, no more books! No more teachers dirty looks! Even I am looking forward to not having to ask my oldest about homework, studying for tests, projects, etc. Time for relaxing by the pool, reading books, and just taking a break.

That being said, summer is a great time to build in some meaningful mathematics with your children.  For the next few posts, we will explore ways you can integrate mathematics into your summer plans without making it feel like “school math”.

Jo Boaler, author of What’s Math Got To Do With It? Helping Children Learn To Love Their Least Favorite Subject, states that one of the most parts of being mathematical is an action called reasoning. This involves explaining why something makes sense (or doesn’t make sense)… This is one of the most important pieces of mathematics, and yet is one of the first teachers say is missing or lost in math programs. And it goes beyond simply asking, “Does your answer make sense?” A student who can reason mathematically realizes that mathematics is a subject that (she) can have her own ideas about, a subject that can invoke different perspectives and methods, and a subject that is connected through organizing concepts and themes. It is not a page of math problems a day or a lesson a day where it feels you are learning something new and different every day of the week.

How can we as parents help our children with reasoning? Make math meaningful in the home. Talk about how you use math in your day. Have your older children help make decisions, such as how much paint you need to buy for a room or how much weed killer you need to buy for your yard. Bake. Use real money (cash!) to purchase items so they get a feel for what money is (Great for addition/subtraction!). These are all ideas we will explore later…

My favorite way to get students engaged in reasoning is called, “What’s Wrong With This?!!!” All junior high kids like to express you are wrong. Why not use it to discuss math? Find advertisements, comments in media, or just conversations you hear that are mathematically unreasonable and have a conversation about why it is wrong. Then get them looking for mistakes as well. It is easy, it makes math interesting, and you are building reasoning skills in your children.

soda .99 centsHere is a pic I took from down the road (of my school) when I was getting gas. So what’s wrong?

The amount advertised (I believe) is meant to represent 99 cents. Does it? You can show 99 cents as 99¢, showing that you could use 99 pennies, or as $0.99, representing that you have one less cent than the value of a dollar. What does 0.99¢ mean? It means you are paying less than one cent; less than a penny. You are paying 99/100 of a penny. Meaning, if I give the cashier a penny, he owes me some change!

Most students won’t see it. In fact, when I really started looking at their decimal work (applying to money) I realized at least 2-3 students per class EACH YEAR were making this same mistake. They weren’t connecting the relationship (and difference) between writing the value in dollars verses cents. They simply knew something about each, and jumbled it together, WITHOUT MAKING SENSE.

Why is this so important? Is it really worth knowing that 0.99¢ is wrong? Well, this idea that money can go “beyond cents” creeps up on us in different places. Take the marquis at a gas station.

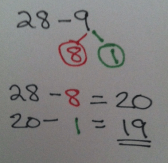
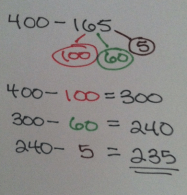
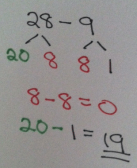
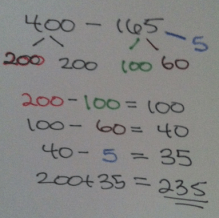
gas prices Letting the fact that this marquis also indicates that I am paying $395 per gallon (Decimal, where are thou???)… $3.95 9/10? What does this mean? Can I pay the 9/10 of a penny? This is actually a great advertising tactic. It is found (See link below for a great article!) that more people will buy if you leave an amount at $0.99 rather than bumping up to the nearest dollar. Significantly more people will buy the $4.99 than the $5.00, because they relate the $4.99 as being closer to $4 than $5. Doesn’t make sense, but that is how we perceive it. So when looking for the cheapest gas, we would gladly take$ 2.19 9/10 versus $2.20, even though the $2.20 location is closer! Don’t believe me? Be mindful of how you choose prices for the next few weeks (And let your kids in on this great experience!) and if you are like me, you will be shocked at how true this is.

Or here…percent financing

0.99% financing. Is that a lot? What if I am buying a car? Would I rather pay 1% financing or 0.99% financing? Why?

Well, this week the cents mistake came up again!whopper

One of my students from last year emailed me this picture with the following message. Hi Mrs. M! I have to tell you that I am ALWAYZ looking for math mistakes now. My mom doesn’t like when I call her out tho.  I found this one and thought you would like to have it. I made my mom look at it and said they would have to give me change for my penny. She thought I was crazy! Ha ha. Thanks for making math fun.

So whether you are out at the store, on vacation, or driving hundreds of miles, look for how math shapes our world. Is the math you are seeing making sense or are there mistakes in the reasoning? You will be surprised; the more you make math meaningful, the more your kids will appreciate it.

Want your child to read more about the money symbols (and why there isn’t a cent sign on the keyboard? Hmmm…), go here! http://www.charlieanderson.com/centsign.htm

For more information regarding the psychology of advertising dollars versus cents, go here! http://www.fastcompany.com/1826172/psychology-behind-sweet-spots-pricing

Summer Math: Does It Make “Cents”?

Top 5 Things NEVER to Do/Say AGAIN When Helping Your Child With Math!!!

Jen Moffett, , , 3 Comments

What we want is to see the child in pursuit of knowledge, and not knowledge in pursuit of the child.   

–George Bernard Shaw

Happy Teacher Appreciation Week!!! I had a blog all good to go with stories from my own edcuational journey, my son’s, and others. Yet it didn’t seem to fit my purpose, which is to support parents in helping their children with math. So I decided to let y’all in on some secrets. Here are the top 5 things teachers wished you would never do (or say) when helping with math. Likewise, here are the top 3 things teachers wished you would always do when supporting your child in math.

Top 5 Things NEVER To Do Again When You Help Your Child With Math

  1. 7cd05c2267bceac7ba2101dc4624d14dNever say, “I wasn’t good at math.” This goes for teachers that do not teach mathematics as well! In fact, on my most recent blog, many responded (on FB) that they were never good at math, nor would they be good at math now. This self-deprecation has to stop NOW!!! This is a cop-out, and it allows your child to think it is okay to be illnumeric (Yeah, totally made up that word.) Would you admit to your child that you couldn’t read or write? Would that be acceptable in your home for your child not to be able to read or write? Heck no! So just stop.
  2. thDVCZDEMMNEVER say the homework is stupid, boring, ridiculous, etc. in front of your child. Jo Boaler, a mathematician out of Stanford University, has done a ton of research on the correlation between student effort and performance in mathematics. Bottom line: the more effort you put in, the better you do. To learn mathematics takes effort, time, and perseverance. You may not like what your child is doing, but relay that message to the teacher, not your child. And please do not write a derogatory note on your child’s homework. This negativity leads your child to believe that he can choose to do some work and skip other work because it is uncomfortable. Would that fly in a job atmosphere? Can I choose to do some of my job-related work and ditch the rest because it is boring? NO, I cannot. Please, support your child at home. Encourage him to try his hardest. “Play” with the problems. And if he goes over the research-based homework time (According to Robert Marzano, 10 minutes per grade level. So for grade 3, 30 min.) take a break, and email his teacher.
  3. 185255772NEVER do the homework for your child! My favorite story about this was with a young lady who was perfectly capable of doing the homework, but got stuck and didn’t know what to do. She asked her father for help. He literally took the pencil from her daughter and wrote it out for her. You could see on the page where she stopped and he began. When I pulled her aside and asked her, she said, “Well, he thought I couldn’t do it so he did it for me.” What did that teach her? When it gets too tough, give up and assume someone else will do it for you? If you want to help, ask questions. But don’t give answers.
  4. stopwatchNEVER EVER attribute brilliance with speed! I am at fault for this. When a toddler can do something quickly, how do we respond? “Wow! You are so SMART.” No, you just already knew how to do it. Children are brought up thinking if they don’t know the answer to a math problem immediately, they are dumb. That is sooo not true!!! Mathematics takes deep focus, diligence, and perseverance. Encourage effort, not speed.
  5. thJ6P17D2JNEVER make excuses for your child to get out of the work. Look, life happens. We teachers get it. Things come up. We love it when you communicate with us, especially when unforeseen circumstances arise. However, your child is still responsible for the work. It may be late, but should still be done. I used to cringe when my middle school student would come in with a big ol’ grin and say, “My mom said I didn’t have to do this and here is the note!” Work it out with the teacher, not your child.

Top 3 Things To Do Right Now To Support Your Child in Math

  1. you can do itEncourage effort. When your child gets frustrated, you can absolutely say that math was tough for you too. BUT MOVE ON. What are the resources she has to support the homework? Was she given examples in notes? Did she already do some of the problems (to look at to refresh her memory)? Are there videos on-line to help? BTW: Many publishers have on-line support via tutorials. Ask your teacher for the link, login and password! Does your teacher offer tutoring? Encourage your child to attend. All of these resources will continue as she moves through education. These are great tools to learn how to access now!
  2. QuestionsAsk questions. My favorite story was of a grandfather who took care of his granddaughter after school. She ended up getting her doctorate (I believe). When asked what contributed to her success, she said it was all the help her grandfather gave her with her homework throughout her time in school. Little did she know, her grandfather was illiterate. He simply helped through questioning. You don’t have to know the math. You need to have good questions to ask.
    • What homework did you have in math today? Show it to me. (Yes, even my child has said his homework is done and…ooops! Still have a few problems left to do…)
    • Tell me what you have tried and where you think you are getting stuck. (Not a question, but a great place to start.)
    • What did you learn in class today that could help you with this? Let’s look it up in the index (if they have a book at home) and see if we can go through the lesson together.
    • Do you have notes from today? Let’s re-read them and see if they can help us.
    • Do you have a problem already done? Let’s go through the steps and see if that refreshes your thoughts.
    • What do you know? Where are you stuck in the problem?
    • Could we go online and look up how to do _______?
    • Who could you call to ask for help? Could you meet with them before school/lunch/etc? (I offered my room for study groups. Kids would come and work together on the homework. Awesome to listen to them help each other!)
    • When does your teacher offer tutoring? Let’s take you to get some support.
  3. Parent teacher ConferenceBe in communication with your teacher. You are your child’s greatest advocate. This is critical in middle and high school, where teachers have up to 200 students a day! Email the teacher when your child is stuck. When he is frustrated. When things get difficult at home. When we had our second child (ten years later), my oldest started slipping in school. I emailed his teachers what was happening, and they were super supportive, giving him the attention and help he needed to get back on track. Teachers do not know what is going on in their students’ outside lives unless you help them know. Help your child by keeping the lines of communication open!

Notice none of my suggestions encouraged you to become a mathematician. Just be a support for your child, encourage effort, and keep in contact with his teacher. These are the greatest gifts you can give a teacher (and your child!). THANKS!!!

To read more from Jo Boaler: http://www.youcubed.org/

Top 5 Things NEVER to Do/Say AGAIN When Helping Your Child With Math!!!