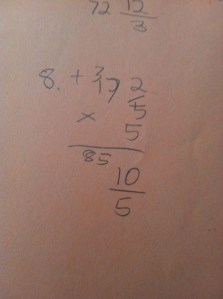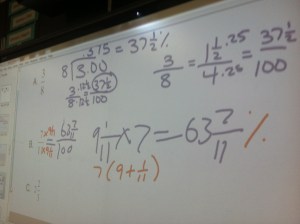The last couple of blogs have highlighted the importance of the distributive property in multiplication for grades 3-8. Let’s refresh ourselves…
Example: 6 x 9 Try it out using the distributive property! (There are many, but I have highlighted two.)
Method 1: Think about the 9 as (10 – 1). Distribute (multiply everything in the parenthesis by) the 6.
6 x (10 – 1) = (6 x 10) – (6 x 1) = 60 – 6 = 54
Method 2: Think about 9 as (4 + 5). Distribute the 6.
6 x (4 + 5) = (6 x 4) + (6 x 5) = 24 + 30 = 54
So you may think, “Jen, where the heck are you going with this?! This is a waste of my time and my child’s time.” Yet here was my son’s homework earlier this year.
He was to multiply 17 2/5 by 5. Most of us learned you MUST convert the mixed number (17 2/5) to an improper fraction, then “multiply tops/multiply bottoms”. Finally change the improper fraction BACK TO A MIXED NUMBER. What a stinkin’ waste of time!
My oldest had the problem done in less than a minute. He got 87. Do you see it? What did he do? I have to admit I didn’t see it at first, and had to ask him. This is what he said (please insert a very monotone voice, since he wasn’t pleased with having to tell his mother his strategy…)
I thought about the 17 2/5 as two parts. 17 + 2/5. I mutliplied 5 times 17 and then 5 times the 2/5. Then I put it back together. (Duh, mom.)
So what does this look like mathematically?
5 x 17 2/5 = 5 x (17 + 2/5)
5 x (17 + 2/5) = (5 x 17) + (5 x 2/5) = 85 + 10/5 = 85 + 2 = 87.
In this case, using the distributive property is MUCH faster than the rules we were taught! And it makes sense! I am using partial products. I break up my number into easier parts, multiply them by the given value, and put it back together.
Here is another example. This came from one of my intervention students (students who are brilliant but don’t excel with the traditional book method in mathematics…) :
You can admire all of his fabulousness, but the piece I want to focus on is 9 1/11 x 7. In red, notice he rewrote it for everyone to understand. Please note he had done it in his head (the blue). All red work was written after to let his class know what he was thinking.
9 1/11 x 7 = 7 x 9 1/11 (commutative property)
7 x 9 1/11 = 7 x (9 + 1/11)
7 x (9 + 1/11) = (7 x 9) + (7 x 1/11) (distributive property)
= 63 + 7/11 = 63 7/11%
Why am I showing you this? As parents, you WILL see the distributive property used with fractions, decimals, and percents. It makes it faster to compute, as students can do most of it in their heads. Most important, when students use the distribute property, I have noticed less “silly” errors. They get it right because it makes sense!
What can you do to support this kind of thinking? Play with numbers. Use a whiteboard. Use the sidewalk with chalk. Use the bathroom mirror with a dry erase pen. Give one problem a day and see how easy it gets to think about multiplication this way.
Here are some starter problems…
7 x 6, 7 x 7, 7 x 8, 7 x 9, 7 x 12 (break the 12 into 10 and 2)
8 x 4, 8 x 6, 8 x 7, 8 x 9, 8 x 12
9 x 4, 9 x 6, 9 x 7, 9 x 8, 9 x 12
3 x 16 (break into 10 + 6), 3 x 17, 3 x 18, …You could go on forever!
2 x 4 1/2, 2 x 5 1/2, 2 x 6 1/2, ….and so on
3 x 4 1/3, 3 x 4 2/3, 3 x 5 1/3, 3 x 5 2/3, …and so on
4 x 3 1/4, 4 x 3 1/2, 4 x 3 3/4, … and so on
If you need more, just look up free worksheets that multiply a mixed number by a whole number. Use one a day!